An introduction to the central limit theorem and sampling techniques

Back

Let’s say we want to understand the life style of different people in different states of India and for that we need to collect the data.

Now we have two options:

Collecting data from each and every person of India
Collecting data from few persons in each state of India.

Obviously, we will choose option 2 because it is easy and practically feasible.

Whenever we select from a subset of the population to make statistical inferences from them and estimate characteristics of the whole population it is called “Sampling”. so here option 2 is our sample.

In this article we are going to cover:

Central limit theorem and why is it important
Features to keep in mind while constructing a sample
Sampling techniques
Probability sampling
Non probability sampling
How do you decide on the type of sampling to use?

What is central limit theorem and why is it important ?

Suppose that we are interested in estimating the average weight among all people. Collecting data for every person in the world is impractical, bordering on impossible. While we can’t obtain a weight measurement from everyone in the population, we can still sample some people. The question now becomes, what can we say about the average weight of the entire population given a single sample.

The Central Limit Theorem addresses this question exactly. Formally, it states that if we sample from a population using a sufficiently large sample size, the mean of the samples (also known as the sample population) will be normally distributed (assuming true random sampling), the mean tending to the mean of the population and variance equal to the variance of the population divided by the size of the sampling. What’s especially important is that this will be true regardless of the distribution of the original population.

Let us take example of population where I have data points between 0 to 21, then my distribution looks like this

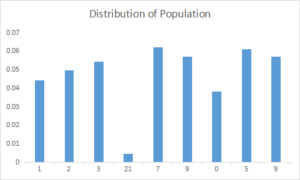
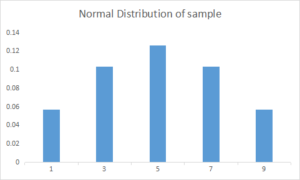
Now if I take only few samples , lets say 1,3,5,7 and 9 and apply normal distribution then my sampling distribution for N=5 is as follows:

Now I repeat this same process with N=3 and have sample points like 1,3 an 5 so my sample distribution is as follows:

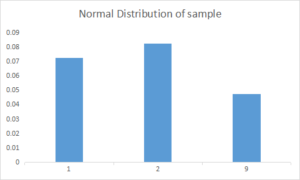
The above plots demonstrate that as the sample size N is increased, the resultant sample mean distribution becomes more normal. Further, the distribution variance also decreases. Keep in mind that the original population that we are sampling from was that weird ugly distribution above.

Further intuition

First when I saw an example of the central limit theorem , I didn’t really understand why it worked. The best intuition that I have came across involves example of playing basket ball video game and tossing a basket ball on opponent’s side court, while playing video game with other team, if my team wins 5 times and other team wins 6 times than it wont be really surprising , similarly if my team wins 7 times and their team wins 5 times than also it is not surprising. But if my team wins 10 times and other team wins 1 time than we might start to question the fairness of basket ball video game.

This is essentially what the normal-ness of the sample distribution represents. For the basket ball example, we are likely to get equal win for N times between two teams. Outcomes farther away from the expected 50/50 result are less likely, and thus less expected. The normal distribution of the sampling distribution captures this concept.

The mean of the sampling distribution will approximate the mean of the true population distribution. Additionally, the variance of the sampling distribution is a function of both the population variance and the sample size used. A larger sample size will produce a smaller sampling distribution variance. This makes intuitive sense, as we are considering more samples when using a larger sample size, and are more likely to get a representative sample of the population. So roughly speaking, if the sample size used is large enough, there is a good chance that it will estimate the population pretty well. Most sources state that for most applications N = 30 is sufficient.

These principles can help us to reason about samples from any population. Depending on the scenario and the information available, the way that it is applied may vary. For example, in some situations we might know the true population mean and variance, which would allow us to compute the variance of any sampling distribution. However, in other situations, such as the original problem we discussed of estimating average human weight, we won’t know the true population mean and variance. Understanding the nuances of sampling distributions and the Central Limit Theorem is an essential first step toward talking many of these problems.

Features to keep in mind while constructing a sample

There are 3 features to keep in mind while constructing a sample.

Consistency : It is important to have consistency in samples for different subsets of population because any change in population should reflect in sample of data representing that population
Diversity : A sample must be as diverse as the population itself to be truly representative of the population and sensitive to the local differences that are unavoidable as we move across the population.
Transparency : Researchers need to discuss limitation of population taken under consideration and must be transparent to communicate the sample of population , so that results of the survey are seen with the right perspective.

Sampling techniques

Probability sampling

Probability sampling is a sampling technique where a researcher sets a selection of a few criteria and chooses members of a population randomly. All the members have an equal opportunity to be a part of the sample with this selection parameter.For example, in a population of 1000 members, every member will have a 1/1000 chance of being selected to be a part of a sample. Probability sampling eliminates bias in the population and gives all members a fair chance to be included in the sample.

There are four types of probability sampling techniques:

Simple random sampling: One of the best probability sampling techniques that helps in saving time and resources, is the Simple Random Sampling method. The entire process of sampling is done in a single step with each subject selected independently of the other members of the population. Each individual has the same probability of being chosen to be a part of a sample as every single member of a population is chosen randomly, merely by chance

For example, in a college of 500 students , if the faculty team decides on conducting team building activities, it is highly likely that they would prefer picking chits out of a bowl. In this case, each of the 500 students has an equal opportunity of being selected.

Pros: In this technique, each member of the population has an equal chance of being selected as subject.

Cons: When there are very large populations, it is often difficult to identify every member of the population and the pool of subjects becomes biased. Dialing numbers from a phone book for instance, may not be entirely random as the numbers, though random, would correspond to a localized region. A sample created by doing so might leave out many sections of the population that are significant to the study.

Use case: Want to study and understand the lifestyle across rural India? While it might not be possible to cover every household, you could draw meaningful insights by building your sample from different districts or villages (depending on the scope).

Cluster sampling : Cluster sampling also involves dividing the population into subgroups, but each subgroup should have similar characteristics to the whole sample. Instead of sampling individuals from each subgroup, you randomly select entire subgroups.If it is practically possible, you might include every individual from each sampled cluster. If the clusters themselves are large, you can also sample individuals from within each cluster using one of the techniques above.

Pros : It allows for research to be conducted with a reduced economy,Cluster sampling reduces variability, It is a more feasible approach and It offers the advantages of random sampling and stratified sampling.

Cons: It is easier to create biased data within cluster sampling, sampling errors can be a major problem,every cluster may have some overlapping data points

Use case : If the Indian government wishes to evaluate the number of immigrants living in the India, they can divide it into clusters based on states such as Gujarat,Maharashtra,Rajasthan, Madhyapradesh etc. This way of conducting a survey will be more effective as the results will be organized into states and provide insightful immigration data.

Systematic sampling: It is similar to simple random sampling, but it is usually slightly easier to conduct. Every member of the population is listed with a number, but instead of randomly generating numbers, individuals are chosen at regular intervals for Example all employees of the company are listed in alphabetical order. From the first 10 numbers, you randomly select a starting point: number 6. from number 6 onwards, every 10th person on the list is selected (6, 16, 26, 36, and so on), and you end up with a sample of 100 people.

Pros: The main advantage of using systematic sampling over simple random sampling is its simplicity. Another advantage of systematic random sampling over simple random sampling is the assurance that the population will be evenly sampled. There exists a chance in simple random sampling that allows a clustered selection of subjects. This can be avoided through systematic sampling.

Cons: The possible weakness of the method that may compromise the randomness of the sample is an inherent periodicity of the list. This can be avoided by randomizing the list of your population entities, as you would randomize a deck of cards for instance, before you proceed with systematic sampling.

Use Case: Suppose a supermarket wants to study buying habits of their customers. Using systematic sampling, they can choose every 10th or 15th customer entering the supermarket and conduct the study on this sample.

Stratified random sampling: Stratified random sampling is a method in which the researcher divides the population into smaller groups that don’t overlap but represent the entire population. While sampling, these groups can be organized and then draw a sample from each group separately. For example, a researcher looking to analyze the characteristics of people belonging to different annual income divisions will create strata (groups) according to the annual family income. Eg – less than $20,000, $21,000 – $30,000, $31,000 to $40,000, $41,000 to $50,000, etc. By doing this, the researcher concludes the characteristics of people belonging to different income groups. Marketers can analyze which income groups to target and which ones to eliminate to create a roadmap that would bear fruitful results.

Pros: This method attempts to overcome the shortcomings of random sampling by splitting the population into various distinct segments and selecting entities from each of them. This ensures that every category of the population is represented in the sample. Stratified sampling is often used when one or more of the sections in the population have a low incidence relative to the other sections.

Cons: Stratified sampling is the most complex method of sampling. It lays down criteria that may be difficult to fulfill and place a heavy strain on your available resources.

Use Case: If 38% of the population is college-educated and 62% of the population have not been to college, then 38% of the sample is randomly selected from the college-educated subset of the population and 62% of the sample is randomly selected from the non-college-going population. Maintaining the ratios while selecting a randomized sample is key to stratified sampling.

Non-probability sampling

In non-probability sampling, the researcher chooses members for research at random. This sampling method is not a fixed or predefined selection process. This makes it difficult for all elements of a population to have equal opportunities to be included in a sample.In most situations, the output of a survey conducted with a non-probable sample leads to skewed results, which may not represent the desired target population. But, there are situations such as the preliminary stages of research or cost constraints for conducting research, where non-probability sampling will be much more useful than the other type.

Four types of non-probability sampling explain the purpose of this sampling method in a better manner:

Convenience sampling : A convenience sample simply includes the individuals who happen to be most accessible to the researcher.This is an easy and inexpensive way to gather initial data, but there is no way to tell if the sample is representative of the population, so it can’t produce generalize results.

Example For example, startups and NGOs usually conduct convenience sampling at a mall to distribute leaflets of upcoming events or promotion of a cause – they do that by standing at the mall entrance and giving out pamphlets randomly.

Pros: The sample is created quickly without adding any additional burden on the available resources.

Cons: The likelihood of this approach leading to a sample that is truly representative of the population is very poor.

Use Case: This method is often used during preliminary research efforts to get a gross estimate of the results, without incurring the cost or time required to select a random sample.

Judgmental or purposive sampling: Judgemental or purposive samples are formed by the discretion of the researcher. Researchers purely consider the purpose of the study, along with the understanding of the target audience.It is often used in qualitative research, where the researcher wants to gain detailed knowledge about a specific phenomenon rather than make statistical inferences. An effective purposive sample must have clear criteria and rationale for inclusion. For instance, when researchers want to understand the thought process of people interested in studying for their master’s degree. The selection criteria will be: “Are you interested in doing your masters in …?” and those who respond with a “No” are excluded from the sample.

Pros : You can take advantage of numerous qualitative research designs, There is still an opportunity to create generalizations from the data,It helps by saving time and money while collecting data,You can target niche demographics to obtain specific data points.

Cons : This process is extremely prone to researcher bias, It may be challenging to defend the representative nature of a sample, The participants in purposive sampling can also manipulate the data being collected,It can be an ineffective method when applied to large population groups, Purposive sampling can still produce inaccurate assumptions.

Use case : when researcher wants to study impact of corona on diabetic patient , he will select only diabetic patient and remove non diabetic patient.

Snowball sampling : If the population is hard to access, snowball sampling can be used to recruit participants via other participants. The number of people you have access to “snowballs” as you get in contact with more people. For example You are researching experiences of homelessness in your city. Since there is no list of all homeless people in the city, probability sampling isn’t possible. You meet one person who agrees to participate in the research, and she puts you in contact with other homeless people that she knows in the area.

Pros: The costs associated with this method are significantly lower, and you will end up with a sample that is very relevant to your study.

Cons: The clear downside of this approach is that you may restrict yourself to only a small, largely homogeneous section of the population.

Use Case: surveys to gather information about HIV Aids. Not many victims will readily respond to the questions. Still, researchers can contact people they might know or volunteers associated with the cause to get in touch with the victims and collect information

Quota Sampling : This type of sampling depends of some pre-set standard. It selects the representative sample from the population. Proportion of characteristics/ trait in sample should be same as population. Elements are selected until exact proportions of certain types of data is obtained or sufficient data in different categories is collected.

Pros: This process can be extended to cover several characteristics and varying degrees of complexity.

Cons: Though the method is superior to convenience and snowball sampling, it does not offer the statistical insights of any of the probability methods.

Use case : If our population has 45% females and 55% males then our sample should reflect the same percentage of males and females.

How do you decide on the type of sampling to use?

For any research, it is essential to choose a sampling method accurately to meet the goals of your study. The effectiveness of your sampling relies on various factors. Here are some steps expert researchers follow to decide the best sampling method.

Jot down the research goals. Generally, it must be a combination of cost, precision, or accuracy.
Identify the effective sampling techniques that might potentially achieve the research goals.
Test each of these methods and examine whether they help in achieving your goal.
Select the method that works best for the research.

Probability sampling techniques are superior, but the costs can be prohibitive. For the initial stages of a study, non-probability sampling techniques might be sufficient to give you a sense of what you’re dealing with. For detailed insights and results that you can bank upon, move on to the more sophisticated techniques as the study gathers pace and takes a more concrete structure.